暗算のコツ～引き算編～

皆さん、こんにちは！

個別指導エミオンです。

今回は、「暗算のコツ」のpart2、引き算編をお伝えしていきます。

この記事は、前回同様小学生の皆さんにも役立つ内容になっていますので、是非ご覧ください。



引き算って、実は小学生の中でも結構苦手な人もいる分野。




その理由は、「ないものをイメージしなくてはならないから」かもしれません。

たとえば、もともと１０個のアメがあって、今は３個になっている。では、何個なくなった？、というような問題

慣れた人は、もちろんすぐに「７個」と答えられるでしょうが、小さい子どもたちにはなかなか難しかったりするのです。

暗算でも似たようなことがいえます。



そういった理由で、足し算の暗算よりも少し苦労する部分もあるかもしれません。

ですが、ちょっとしたコツで格段に計算が楽になるんです。

是非、マスターしていきましょう。

１桁ー１桁

ここでは、答えが「ー（マイナス）」になるものは扱いません。

まずは、基礎的な引き算を完璧にできるようになりましょう。

「１桁ー１桁」の計算は、多くの人にとって簡単といえるでしょう。

実際に小学校で扱う「１桁ー１桁」の計算のパターンは、以下のものだけ。

「９－９」「９－８」「９－７」「９－６」「９－５」「９－４」「９－３」「９－２」「９－１」「９－０」
「８－８」「８－７」「８－６」「８－５」「８－４」「８－３」「８－２」「８－１」「８－０」
「７－７」「７－６」「７－５」「７－４」「７－３」「７－２」「７－１」「７－０」
「６－６」「６－５」「６－４」「６－３」「６－２」「６－１」「６－０」
「５－５」「５－４」「５－３」「５－２」「５－１」「５－０」
「４－４」「４－３」「４－２」「４－１」「４－０」
「３－３」「３－２」「３－１」「３－０」
「２－２」「２－１」「２－０」
「１－１」「１－０」
「０－０」

ここができないと勿論先に進めません。

足し算の「１桁＋１桁」同様、問題を見て瞬時に答えが導き出せるように、徹底的にトレーニングしましょう。

余談ですが、実は、個別指導エミオンの近くには、同じグループの幼児教室があり、幼稚園に行っている子どもたちに計算を教える機会などがあるのですが、引き算が苦手な子には、以下の２パターンを推奨しています。

①足し算にしてしまう

「７－２＝□」といった計算の場合、「７＝□＋２」という形にします。

そうすると、多くの子ども達はスラスラ解いてくれるようになります。

やはり、引き算のイメージはなかなかつかみづらいようです。

②指を使う

お決まりのやり方ですね。

指を使うとよくない、といった話も耳にしますが、私は全く問題ないと思います。

これは、筆算なんかせずに暗算で解けるようになりなさい、と言っているようなものです。

暗算もできればそれに越したことはないですが、筆算でしかできなくても数学や算数の能力には影響ありません。

そのような弊害を気にする前に、どんどん練習をしていくほうが確実に早く慣れることができるでしょう。

２桁ー１桁

ここからが本題です。

基本的につまづく人が多くなるのが、この辺から。

いわゆる、「繰り下がり」が出てくるからですね。

まずは、繰り下がりがあるかないかを問題を見てすぐに判断しましょう。

繰り下がりのない引き算

これは、問題ないはず。

「１５－２」といった問題で考えてみましょう。

①繰り下がりがないので、十の位はもうそのまま。

頭の中では、「１□」という答えをイメージします。
（※できる限り口に出さず、紙にも書かず、頭の中で数字を置けるように意識しましょう）

②一の位同士を計算しましょう。

「５－２＝３」ですね。

よって、答えは「１３」と出てきます。

「１桁ー１桁」の計算とほぼ同じです。

繰り下がりのある引き算

たとえば、「１３－９」の問題を考えてみましょう。

瞬時に「４」と答えが出るでしょうか。

当たり前のことですが、「□３ー９」は、□に何が入ろうとも答えの一の位は「４」になります。

この感覚（引き算の答えにおいて、一の位は瞬時に決まるという感覚）を大切にしてください。

これについても、ほぼ暗記です。

このパターンを覚えるのです。


覚えるほどトレーニングするとでもいった方が分かりやすいでしょうか。

繰り下がりのある場合だけが厄介なので、覚えるべきは以下の３６通りだけ。

「□１ー２」「□１ー３」「□１ー４」「□１ー５」「□１ー６」「□１ー７」「□１ー８」「□１ー９」
「□２ー３」「□２ー４」「□２ー５」「□２ー６」「□２ー７」「□２ー８」「□２ー９」
「□３ー４」「□３ー５」「□３ー６」「□３ー７」「□３ー８」「□３ー９」
「□４ー５」「□４ー６」「□４ー７」「□４ー８」「□４ー９」
「□５ー６」「□５ー７」「□５ー８」「□５ー９」
「□６ー７」「□６ー８」「□６ー９」
「□７ー８」「□７ー９」
「□８ー９」

これらの時に、答えの一の位の数字がどうなるか、確実に瞬時に答えを言えるようになりましょう。

では、パターンを覚えたと仮定して、次に「５３－９」の場合を考えてみましょう。

①答えの十の位を決定します。

頭の中で、繰り下がりがあると判断した瞬間に、答えは十の位の「５」から「１」を引いて「４□」になることが決まります。

「２」を引くことはありえないので、心配なく「１」を引きましょう。

②あとは、一の位同士を考えるだけ。

「□３ー９」の場合は、答えの一の位は必ず「４」になるので、「４４」が答えとわかります。

２桁ー２桁

「２桁ー２桁」の暗算までできればバッチリです。

では、順にみていきましょう。

この場合も、答えがマイナスになるものは除きます。

繰り下がりがない場合

これは超簡単。

「５７－３２」といった問題で考えます。

やることは、①十の位と一の位にわけて引き算するのみ

十の位は、「５－３＝２」、一の位は「７－２＝５」、つまり答えは「２５」です。

繰り下がりのある場合

答えがマイナスになる場合は考えないので、「７２－３５」で考えてみましょう。

十の位から考えます。

①まずは、普通に十の位同士を引き算

「７－３＝４」

②次に、①の答えからさらに「１」を引きます

やはりこの時も無条件で「１」を引いてください。

「４－１＝３」この時点で、答えは「３□」になるとイメージします。

③最後に、一の位同士の引き算

「□２ー□５」の場合も先ほどの「２桁-１桁」のパターンが使えます。

「□２ー□５」の答えの一の位は、必ず「７」になるので、答えは「３７」となります。

総括

いかがでしたか。

引き算も足し算と大きく異なることはありません。

一番大切なのは、答えの一の位を瞬時に判断できること。

これができれば、引き算の暗算はスムーズに行えるはずです。

足し算・引き算の暗算が完璧になった人は、いよいよ掛け算・割り算の暗算に入っていきましょう。

～今からの努力が、未来を創る～

月～日まで、毎日開室！毎日自習可！
２４時間３６５日、
徹底的にサポートいたします。

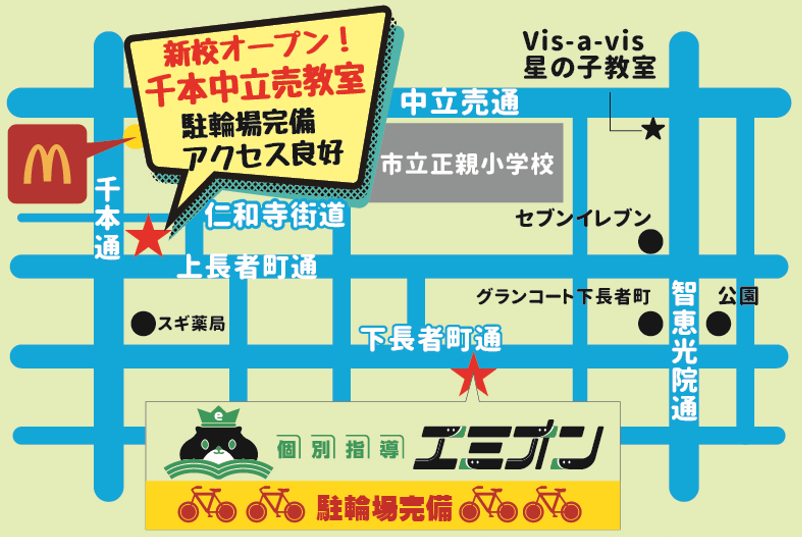
【住所】
《千本中立売教室（メイン教室）》
〒602-8283
京都市上京区仲御霊町７７
ベルム西陣　1階
TEL:075-432-8133（共通）

《下長者町教室（本部教室）》
〒602-8179
京都市上京区下長者町通裏門西入坤高町８６
TEL：075-432-8133（共通）

【授業時間】
＜月～金＞
１限　１６：３０～１８：１０
２限　１８：２０～２０：００
３限　２０：１０～２１：５０

＜土・日＞
A　　　 ９：１０～１０：５０
B　　 １１：００～１２：４０
C　　 １２：５０～１４：３０
D　　 １４：４０～１６：２０
１限　１６：３０～１８：１０
２限　１８：２０～２０：００
３限　２０：１０～２１：５０

【対象】
中学生・高校生・既卒生

【通塾生徒の主な学校】
二条中・上京中・北野中・衣笠中
京都聖母学院中・京産大附属中・
立命館中・京都精華学園中・
京都先端科学大学附属中・洛星中
堀川高校・嵯峨野高校・西京高校・
山城高校・鴨沂高校

【教室へのお問合せは】
①当塾ホームページからお問い合わせください
https://e-emion.jp/toiawase/

②当塾までお電話ください
075-432-8133
（年中無休１４：００～２２：００）